[ad_1]
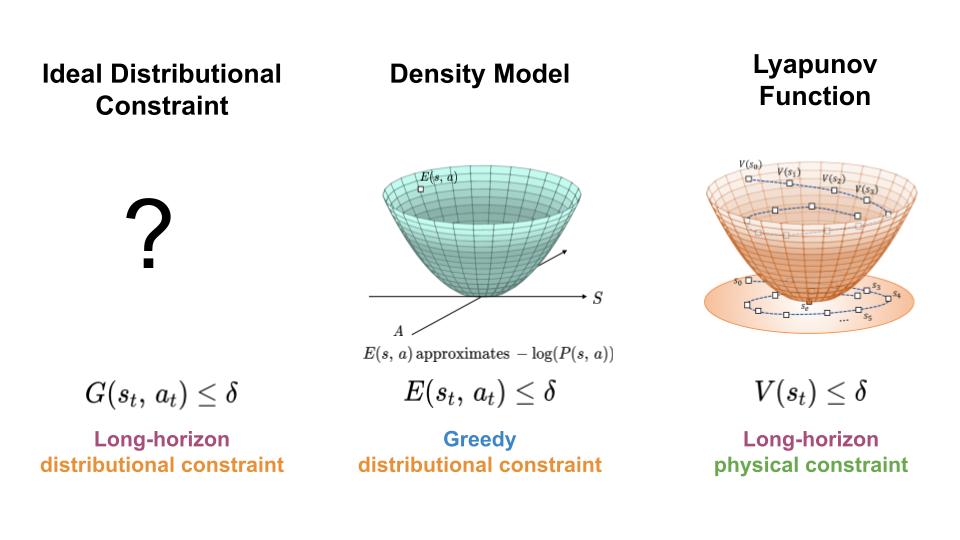
To deal with the distribution shift expertise by learning-based controllers, we search a mechanism for constraining the agent to areas of utmost knowledge density all by its trajectory (left). Correct proper right here, we current an method which achieves this purpose by combining selections of density fashions (center) and Lyapunov choices (right).
With a operate to make the most of machine discovering out and reinforcement discovering out in controlling exact world methods, we should at all times design algorithms which not solely obtain good effectivity, nevertheless in addition to work together with the system in a protected and dependable method. Most prior work on safety-critical administration focuses on sustaining the protection of the bodily system, e.g. avoiding falling over for legged robots, or colliding into obstacles for autonomous vehicles. Nonetheless, for learning-based controllers, there may be one totally different present of security concern: on account of machine discovering out fashions are solely optimized to output relevant predictions on the instructing knowledge, they’re susceptible to outputting inaccurate predictions when evaluated on out-of-distribution inputs. Thus, if an agent visits a state or takes an motion which can be very totally utterly totally different from these contained in the instructing knowledge, a learning-enabled controller may “exploit” the inaccuracies in its realized element and output actions which is perhaps suboptimal and even harmful.
To stop these potential “exploitations” of mannequin inaccuracies, we advocate a mannequin new framework to motive concerning the protection of a learning-based controller with respect to its instructing distribution. The central thought behind our work is to view the instructing knowledge distribution as a security constraint, and to attract on gadgets from administration thought to deal with the distributional shift skilled by the agent all by means of closed-loop administration. Additional considerably, we’ll cope with how Lyapunov stability is probably unified with density estimation to supply Lyapunov density fashions, a mannequin new form of security “barrier” operate which is perhaps utilized to synthesize controllers with ensures of defending the agent in areas of utmost knowledge density. Ahead of we introduce our new framework, we’ll first give a prime degree view of current methods for guaranteeing bodily security by barrier operate.
In administration thought, a central subject of research is: given acknowledged system dynamics, $s_{t+1}=f(s_t, a_t)$, and acknowledged system constraints, $s in C$, how can we design a controller that’s assured to maintain up the system all by means of the specified constraints? Correct proper right here, $C$ denotes the set of states which is perhaps deemed protected for the agent to go to. This draw back is troublesome on account of the desired constraints needs to be utterly glad over the agent’s total trajectory horizon ($s_t in C$ $forall 0leq t leq T$). If the controller makes use of a easy “grasping” technique of avoiding constraint violations inside the next time step (not taking $a_t$ for which $f(s_t, a_t) notin C$), the system should nonetheless find yourself in an “irrecoverable” state, which itself is taken into consideration protected, nonetheless will inevitably result in an unsafe state ultimately whatever the agent’s future actions. With a operate to keep away from visiting these “irrecoverable” states, the controller should make use of an extra “long-horizon” strategy which entails predicting the agent’s total future trajectory to keep away from security violations at any diploma ultimately (keep away from $a_t$ for which all potential ${ a_{hat{t}} }_{hat{t}=t+1}^H$ result in some $bar{t}$ the place $s_{bar{t}} notin C$ and $t<bar{t} leq T$). Nonetheless, predicting the agent’s full trajectory at each step could be very computationally intensive, and typically infeasible to carry out on-line all by means of run-time.
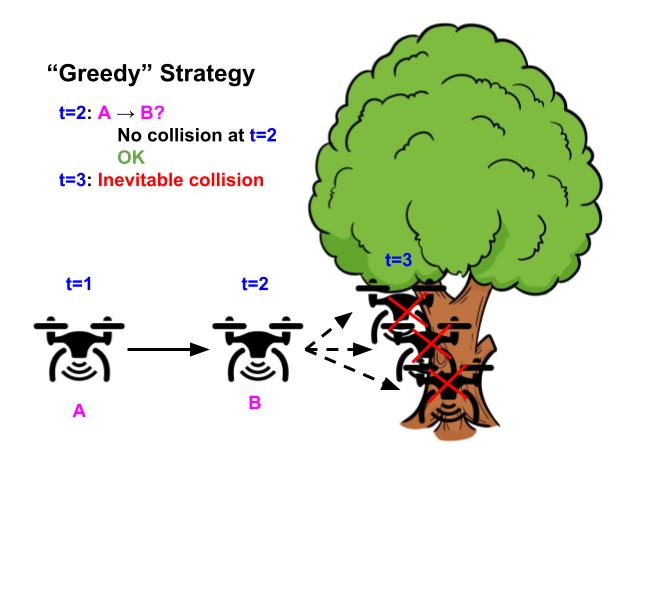
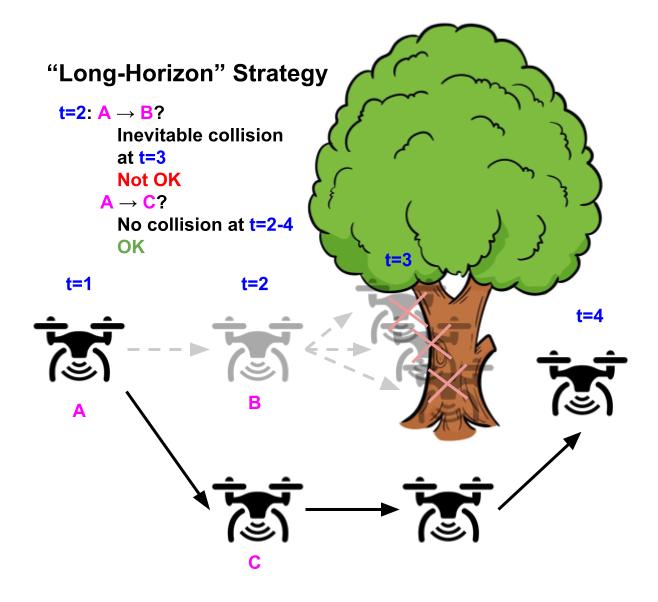
Illustrative event of a drone whose purpose is to fly as straight as potential whereas avoiding obstacles. Utilizing the “grasping” technique of avoiding security violations (left), the drone flies straight on account of there’s no impediment inside the next timestep, nonetheless inevitably crashes ultimately on account of it would in all probability’t flip in time. In distinction, utilizing the “long-horizon” strategy (right), the drone turns early and successfully avoids the tree, by contemplating your full future horizon strategy forward for its trajectory.
Administration theorists kind out this disadvantage by designing “barrier” choices, $v(s)$, to constrain the controller at every step (solely permit $a_t$ which fulfill $v(f(s_t, a_t)) leq 0$). With a operate to make sure the agent stays protected all by its total trajectory, the constraint induced by barrier choices ($v(f(s_t, a_t))leq 0$) prevents the agent from visiting each unsafe states and irrecoverable states which inevitably result in unsafe states ultimately. This method primarily amortizes the computation of attempting into the long run for inevitable failures when designing the protection barrier operate, which solely should be accomplished as shortly as and is probably computed offline. This vogue, at runtime, the safety solely ought to make use of the grasping constraint satisfaction strategy on the barrier operate $v(s)$ with the intention to guarantee security for all future timesteps.
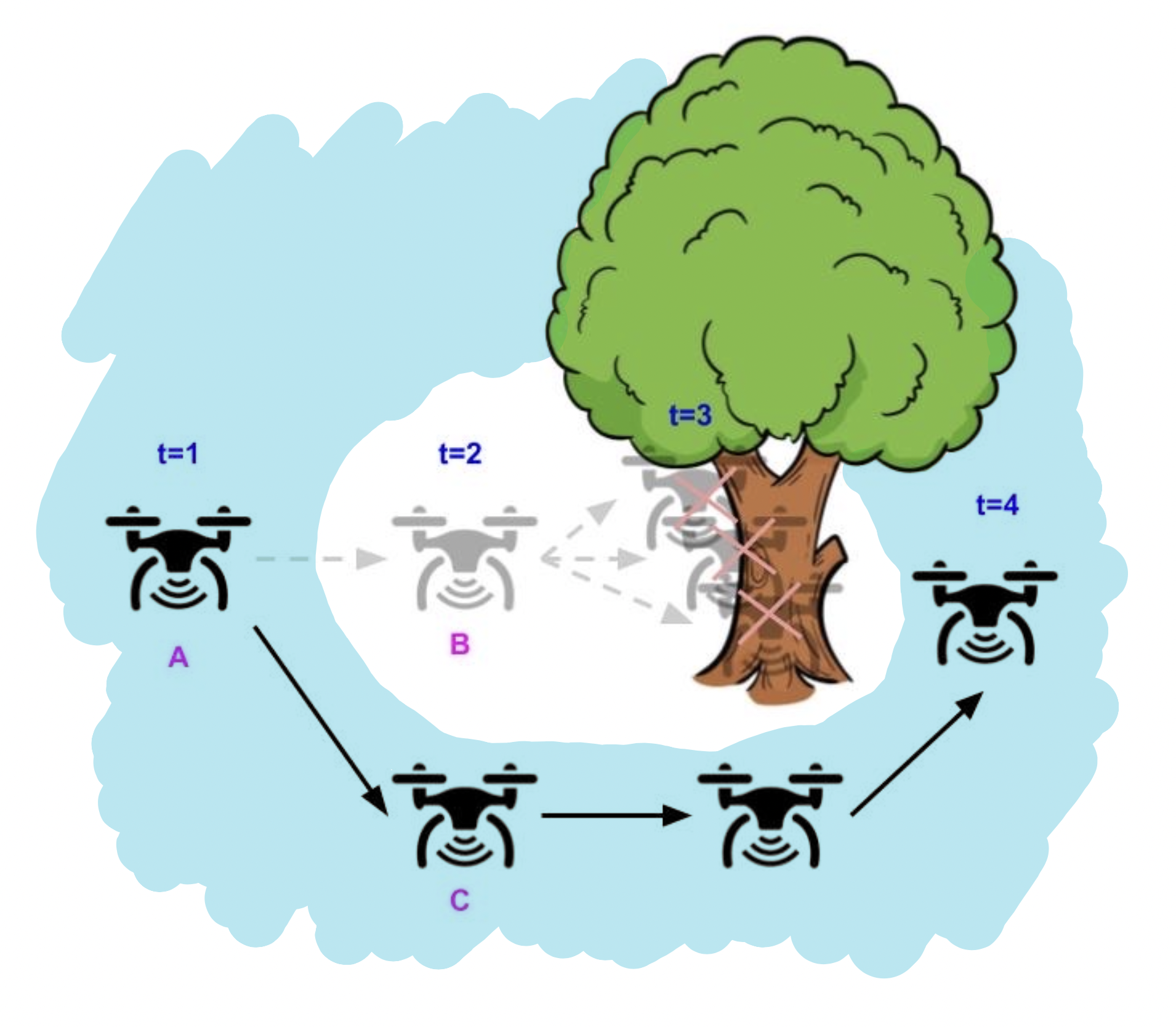
The blue house denotes the of states allowed by the barrier operate constraint, $ v(s) leq 0$. Utilizing a “long-horizon” barrier operate, the drone solely ought to greedily be certain that the barrier operate constraint $v(s) leq 0$ is totally glad for the following state, with the intention to keep away from security violations for all future timesteps.
Correct proper right here, we used the notion of a “barrier” operate as an umbrella time interval to make clear a great deal of totally differing kinds of choices whose functionalities are to constrain the controller with the intention to make long-horizon ensures. Some express examples embody administration Lyapunov choices for guaranteeing stability, administration barrier choices for guaranteeing common security constraints, and the worth operate in Hamilton-Jacobi reachability for guaranteeing common security constraints beneath exterior disturbances. Additional lately, there has furthermore been some work on discovering out barrier choices, for settings the place the system is unknown or the place barrier choices are troublesome to design. Nonetheless, prior works in each typical and learning-based barrier choices are primarily centered on making ensures of bodily security. All through the next half, we’ll cope with how we’re able to lengthen these concepts to deal with the distribution shift skilled by the agent when utilizing a learning-based controller.
To stop mannequin exploitation attributable to distribution shift, many learning-based administration algorithms constrain or regularize the controller to stop the agent from taking low-likelihood actions or visiting low likelihood states, for instance in offline RL, model-based RL, and imitation discovering out. Nonetheless, most of those strategies solely constrain the controller with a single-step estimate of the data distribution, akin to the “grasping” technique of defending an autonomous drone protected by stopping actions which causes it to crash inside the next timestep. As we seen contained in the illustrative figures above, this technique merely is just not sufficient to make it possible for the drone is simply not going to crash (or go out-of-distribution) in a single totally different future timestep.
How can we design a controller for which the agent is assured to remain in-distribution for its total trajectory? Recall that barrier choices is perhaps utilized to ensure constraint satisfaction for all future timesteps, which is precisely the form of assure we hope to make just about regarding the knowledge distribution. Primarily based completely on this commentary, we advocate a mannequin new form of barrier operate: the Lyapunov density mannequin (LDM), which merges the dynamics-aware facet of a Lyapunov operate with the data-aware facet of a density mannequin (it’s the actuality is a generalization of each kinds of operate). Analogous to how Lyapunov choices retains the system from turning into bodily unsafe, our Lyapunov density mannequin retains the system from going out-of-distribution.
An LDM ($G(s, a)$) maps state and motion pairs to unfavorable log densities, the place the values of $G(s, a)$ signify the proper knowledge density the agent is ready to protect above all by its trajectory. It is perhaps intuitively thought-about a “dynamics-aware, long-horizon” transformation on a single-step density mannequin ($E(s, a)$), the place $E(s, a)$ approximates the unfavorable log likelihood of the data distribution. Since a single-step density mannequin constraint ($E(s, a) leq -log(c)$ the place $c$ is a cutoff density) might nonetheless permit the agent to go to “irrecoverable” states which inevitably causes the agent to go out-of-distribution, the LDM transformation will improve the worth of these “irrecoverable” states till they become “recoverable” with respect to their up to date worth. As a consequence of this, the LDM constraint ($G(s, a) leq -log(c)$) restricts the agent to a smaller set of states and actions which excludes the “irrecoverable” states, thereby ensuring the agent is ready to preserve in excessive data-density areas all by its total trajectory.
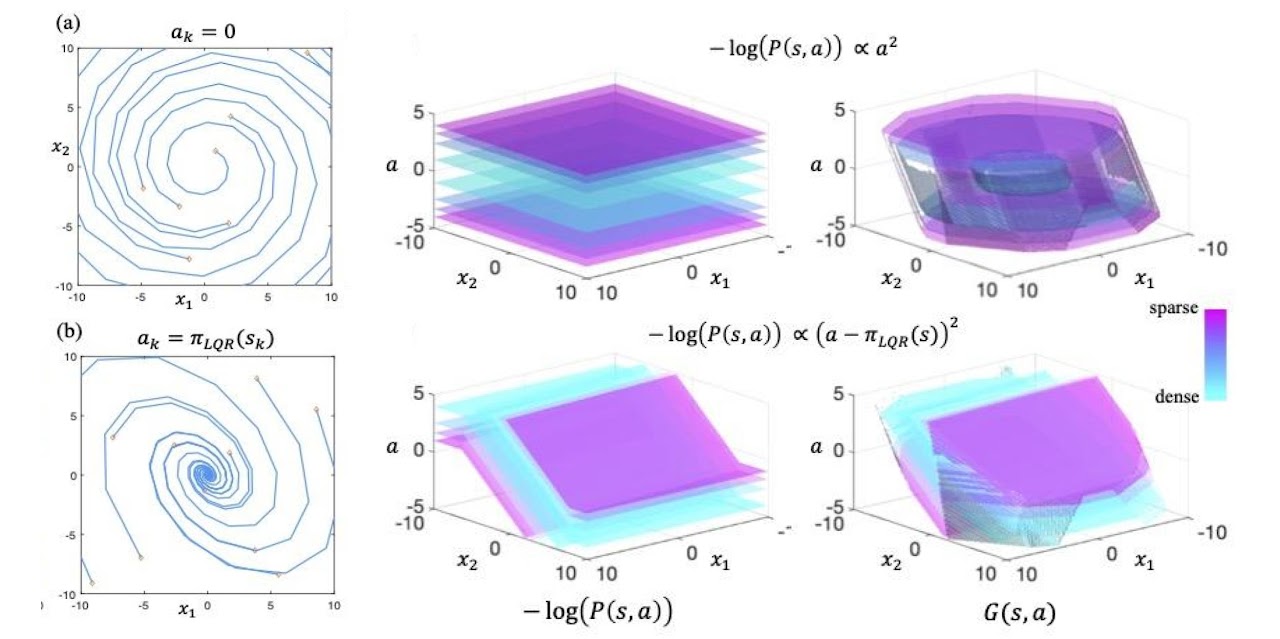
Event of information distributions (center) and their related LDMs (right) for a 2D linear system (left). LDMs is probably considered “dynamics-aware, long-horizon” transformations on density fashions.
How precisely does this “dynamics-aware, long-horizon” transformation work? Given a knowledge distribution $P(s, a)$ and dynamical system $s_{t+1} = f(s_t, a_t)$, we outline the next because of the LDM operator: $mathcal{T}G(s, a) = max{-log P(s, a), min_{a’} G(f(s, a), a’)}$. Suppose we initialize $G(s, a)$ to be $-log P(s, a)$. Beneath one iteration of the LDM operator, the worth of a state motion pair, $G(s, a)$, can every preserve at $-log P(s, a)$ or enhance in worth, relying on whether or not or not or not the worth on the good state motion pair inside the next timestep, $min_{a’} G(f(s, a), a’)$, is larger than $-log P(s, a)$. Intuitively, if the worth on the good subsequent state motion pair is larger than the present $G(s, a)$ worth, which signifies that the agent is unable to stay on the present density diploma regardless of its future actions, making the present state “irrecoverable” with respect to the present density diploma. By rising the present the worth of $G(s, a)$, we’re “correcting” the LDM such that its constraints wouldn’t embody “irrecoverable” states. Correct proper right here, one LDM operator substitute captures the have an effect on of attempting into the long run for one timestep. If we repeatedly apply the LDM operator on $G(s, a)$ till convergence, the ultimate phrase LDM is probably freed from “irrecoverable” states contained in the agent’s total future trajectory.
To make the most of an LDM in administration, we’re able to put collectively an LDM and learning-based controller on the equal instructing dataset and constrain the controller’s motion outputs with an LDM constraint ($G(s, a)) leq -log(c)$). On account of the LDM constraint prevents each states with low density and “irrecoverable” states, the learning-based controller shall be capable of keep away from out-of-distribution inputs all by the agent’s total trajectory. Moreover, by deciding on the cutoff density of the LDM constraint, $c$, the customer is ready to administration the tradeoff between defending within the route of mannequin error vs. flexibility for performing the specified train.
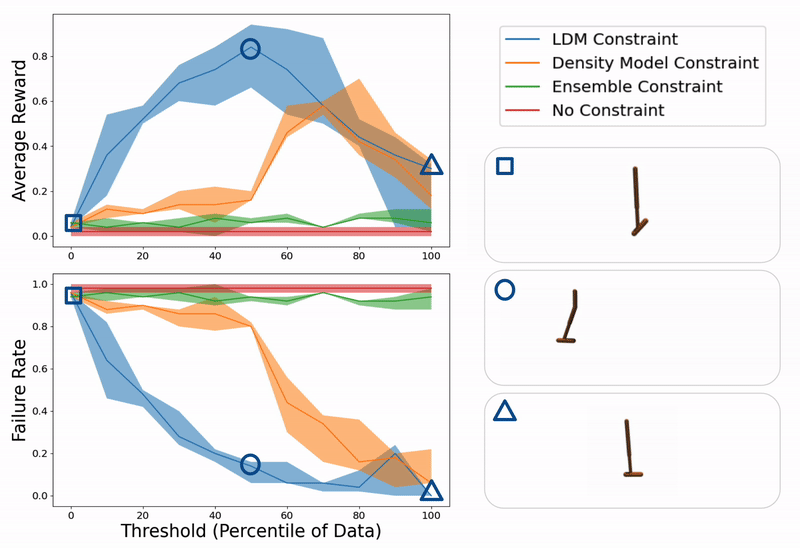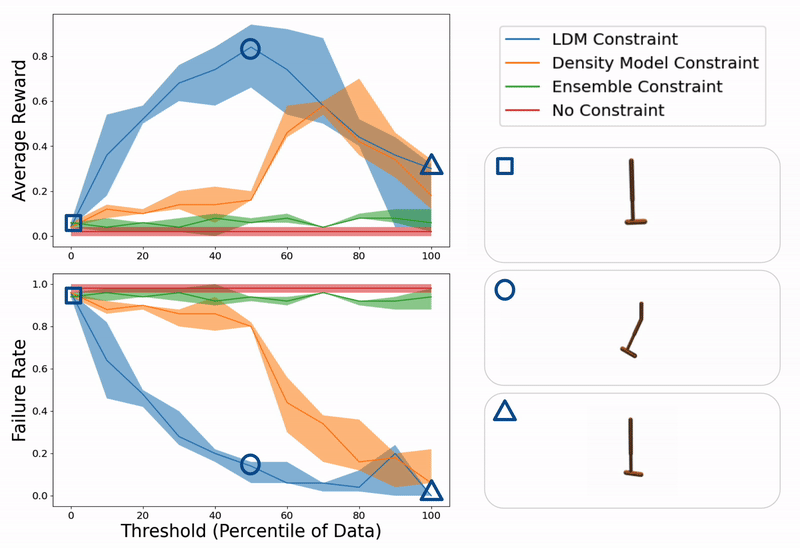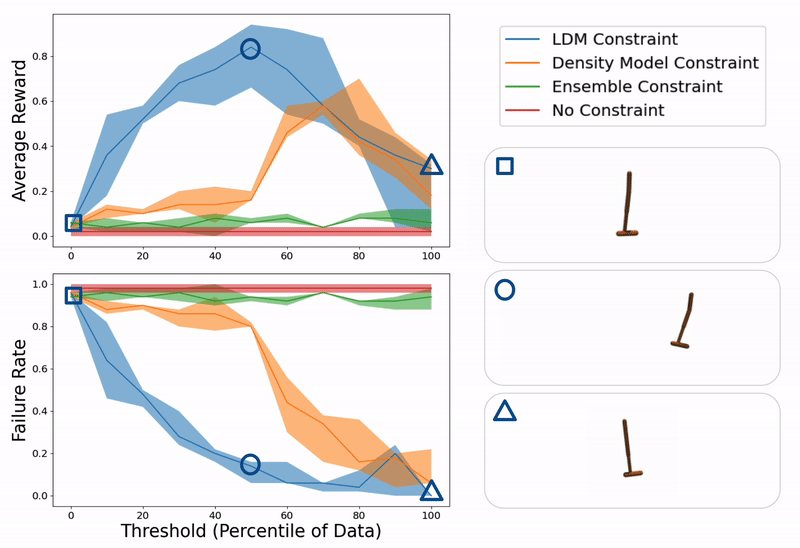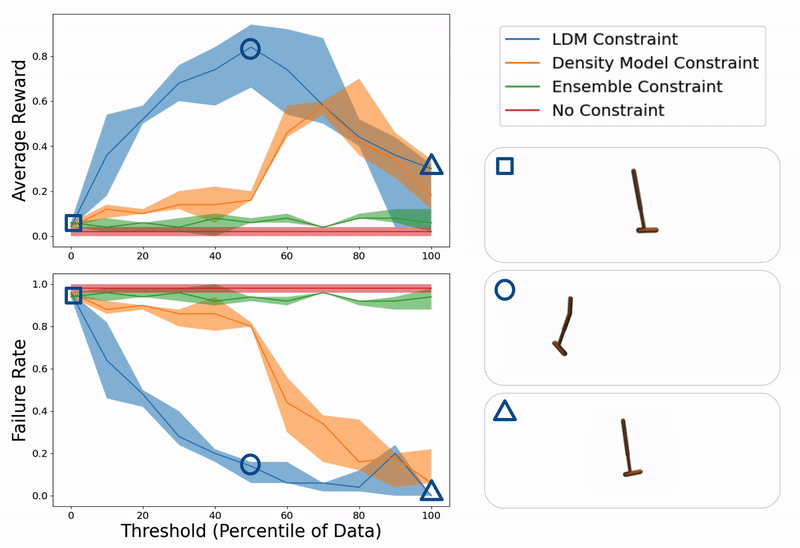
Event analysis of ours and baseline strategies on a hopper administration train for quite a few values of constraint thresholds (x- axis). On the changing into, we present event trajectories from when the sting is simply too low (hopper falling over attributable to extreme mannequin exploitation), good (hopper successfully hopping in path of goal location), or too excessive (hopper standing nonetheless attributable to over conservatism).
To date, we now have solely talked concerning the properties of a “good” LDM, which is probably discovered if we had oracle entry to the data distribution and dynamical system. In adjust to, although, we approximate the LDM utilizing solely knowledge samples from the system. This causes an issue to return up: though the place of the LDM is to stop distribution shift, the LDM itself may endure from the unfavorable outcomes of distribution shift, which degrades its effectiveness for stopping distribution shift. To know the diploma to which the degradation occurs, we analyze this draw back from each a theoretical and empirical perspective. Theoretically, we present even when there are errors contained in the LDM discovering out course of, an LDM constrained controller stays to have the ability to protect ensures of defending the agent in-distribution. Albeit, this assure is a bit weaker than the distinctive assure supplied by an ideal LDM, the place the quantity of degradation depends upon upon the dimensions of the errors contained in the discovering out course of. Empirically, we approximate the LDM utilizing deep neural networks, and present that utilizing a realized LDM to constrain the learning-based controller nonetheless gives effectivity enhancements in contrast with utilizing single-step density fashions on plenty of domains.
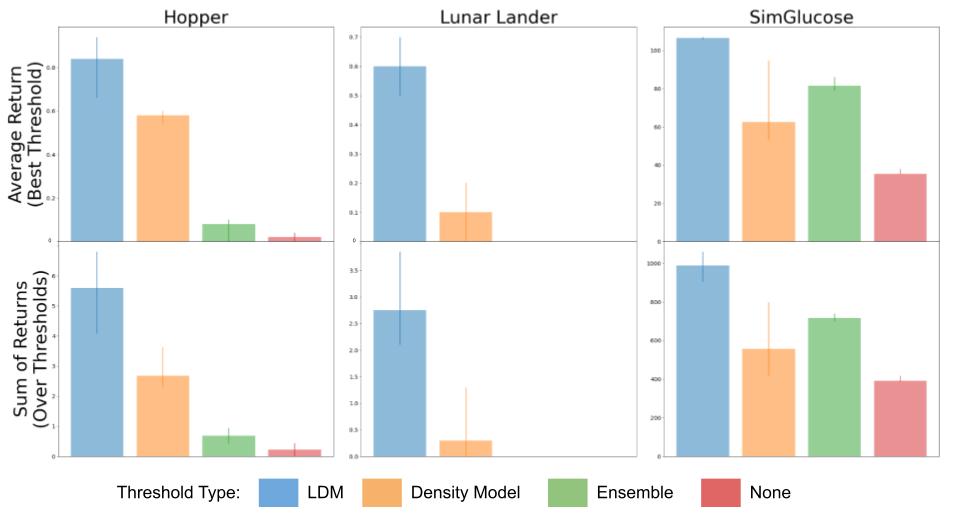
Analysis of our strategy (LDM) in contrast with constraining a learning-based controller with a density mannequin, the variance over an ensemble of fashions, and no constraint in the least on plenty of domains together with hopper, lunar lander, and glucose administration.
At present, actually one in all many largest challenges in deploying learning-based controllers on exact world methods is their potential brittleness to out-of-distribution inputs, and lack of ensures on effectivity. Conveniently, there exists an unlimited physique of labor in administration thought centered on making ensures about how methods evolve. Nonetheless, these works normally deal with making ensures with respect to bodily security necessities, and assume entry to an applicable dynamics mannequin of the system together with bodily security constraints. The central thought behind our work is to in its place view the instructing knowledge distribution as a security constraint. This permits us to make the most of these concepts in controls in our design of learning-based administration algorithms, thereby inheriting each the scalability of machine discovering out and the rigorous ensures of administration thought.
This submit depends on the paper “Lyapunov Density Fashions: Constraining Distribution Shift in Discovering out-Based totally Administration”, launched at ICML 2022. You
uncover additional particulars in our paper and on our web site. We thank Sergey Levine, Claire Tomlin, Dibya Ghosh, Jason Choi, Colin Li, and Homer Walke for his or her priceless concepts on this weblog submit.
[ad_2]
